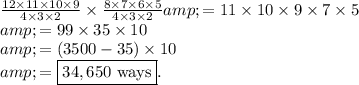Question

thomas, carrie and lenny each captain a different one of three hockey teams. each captain will choose four players from a pool of 12 players, with each player chosen for only one team. how many different ways can the teams be formed?

Answer 1

Thomas can choose any 4 out of 12 players, which is
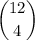`$\binom{12}{4}$` distinct possibilities for a team. Carrie can choose any 4 out of the remaining 8 players, which is
`$\binom{8}{4}$` distinct possibilities for a team. Lenny has only 1 choice for his team, whichever 4 have not yet been chosen. Combining all this yields

`(12*11*10*9)/(4*3*2)*(8*7*6*5)/(4*3*2) &= 11* 10 * 9 * 7 * 5 \\&= 99* 35* 10 \\&= (3500-35)* 10 \\&= \boxed{34,650\text{ ways}}.`