1 Answer

Fernando Nogueira · Answer 1 · 2023-11-15T06:00:05+0000

Answer:

C) Domain: all real numbers x except x = ±2

E) f(x) → ∞ as x → -2⁻ and as x → 2⁺, f(x) → -∞ as x → -2⁺ and as x → 2⁻

Explanation:

Given function:

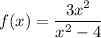
f(x)=(3x^2)/(x^2-4)

The domain of a function is the set of all possible input values (x-values).

A rational function is undefined when the denominator is equal to zero.

The denominator of the given function is zero when:

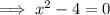
$\implies x^2-4=0$

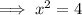
$\implies x^2=4$

$\implies √(x^2)=√(4)$

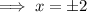
$\implies x= \pm 2$

Therefore the domain of the function is:

The excluded x-values are x = -2 and x = 2.

To find the behaviour of the function near the excluded x-values, input values of x that are very near either side of excluded values:

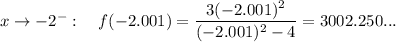
$x \rightarrow -2^-: \quad f(-2.001)=(3(-2.001)^2)/((-2.001)^2-4)=3002.250...$

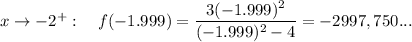
$x \rightarrow -2^+: \quad f(-1.999)=(3(-1.999)^2)/((-1.999)^2-4)=-2997,750...$

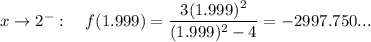
$x \rightarrow 2^-: \quad f(1.999)=(3(1.999)^2)/((1.999)^2-4)=-2997.750...$

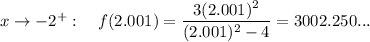
$x \rightarrow -2^+: \quad f(2.001)=(3(2.001)^2)/((2.001)^2-4)=3002.250...$

Therefore, the behaviour of the function near the excluded x-values:

Your comment on this question: