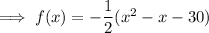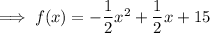Question

Write a function in any form that would match the graph shown below

Answer 1

`f(x)=-(1)/(2)x^2+(1)/(2)x+15`

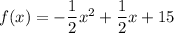
Explanation:

The given graph is a parabola with:

• x-intercepts: (-5, 0) and (6, 0)
• y-intercept: (0, 15)

Therefore, a suitable function that would match the graph is a quadratic function.

`\boxed{\begin{minipage}{6 cm}\underline{Intercept form of a quadratic function}\\\\$f(x)=a(x-p)(x-q)$\\\\where:\\ \phantom{ww}$\bullet$ $p$ and $q$ are the $x$-intercepts. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}`

As the parabola opens downwards, a < 0.

`\implies f(x)=-a(x-p)(x-q)`

Substitute the x-intercepts into the formula:

`\implies f(x)=-a(x-(-5))(x-6)`

`\implies f(x)=-a(x+5)(x-6)`

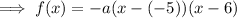
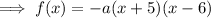
To find the value of a, substitute the y-intercept into the equation:

`\implies 15=-a(0+5)(0-6)`

`\implies 15=-a(5)(-6)`

`\implies 15=-a \cdot -30`

`\implies 15=30a`

`\implies a=(15)/(30)=(1)/(2)`

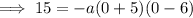
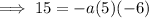
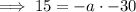
Therefore the quadratic function that models the given graph in intercept form is:

`\implies f(x)=-(1)/(2)(x+5)(x-6)`

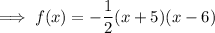
To write the function in standard form, expand the brackets:

`\implies f(x)=-(1)/(2)(x^2-x-30)`

`\implies f(x)=-(1)/(2)x^2+(1)/(2)x+15`