Question

Use decomposition to find the area of the figure.

10 yd
8 yd
The area is
13 yd
square yards.

Answer 1

Answer: 92 yd²

Explanation:

Decomposition means to break the shape into parts, but it's not necessary to break apart.

This is a trapezoid turned sideways A=1/2(b1+b1)h

b1=10

b2=13

h=8

A=1/2(10+13)8 =92 yd²

if you decompose, you can make the top a triangle and bottom a rectangle.

A(triangle) = 1/2(b)(h) b=3 h=8

1/2(b)(h)

= 12

A(rectangle)=bh b=10 h=8

=10*8

=80

Add the 2 and you get 92 again

Answer 2

The area is 92 square yards.

Explanation:

We can decompose this figure into a rectangle and a triangle.

First, we can find the area of the rectangle.

A(rect) = length × width

A(rect) = 10 × 8

A(rect) = 80 yd²

Next, we can find the area of the triangle.

A(triangle) = (1/2) × base × height

`A(\text{triangle}) = (1)/(2) \, (13 - 10) * 8`

`A(\text{triangle}) = (3)/(2) * 8`

`A(\text{triangle}) = 12 \text{ yd}^2`

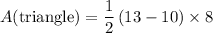
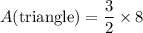
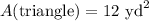
Finally, we can add the two shapes' areas to get the area of the entire figure.

A = A(rect) + A(triangle)

A = 80 yd² + 12 yd²

A = 92 yd²