Question

Suppose that the length of research papers is uniformly distributed from 12 to 25 pages. We survey a class in which 55 research papers were turned in to a professor. The 55 research papers are considered a random collection of all papers. We are interested in the average length of the research papers.

A.) Give the distribution of X. (round your standard deviation to two decimal places. X
∼ N (18.5, _____)
B.) Give the distribution of SumX. Round your standard deviation to two decimal places. SumX
∼ (1017.5, _____).
C). Calculate the probability that the professor will need to read a total of more than 1080 pages. _____

Answer 1

A.) X ~ N(18.5, 3.75)

B.) SumX ~ N(1017.5,27.8).

C.) 0.0122 = 1.22% probability that the professor will need to read a total of more than 1080 pages.

Step-by-step explanation:

Uniform distribution:

A distribution is called uniform if each outcome has the same probability of happening.

The uniform distributon has two bounds, a and b.

The mean is given by:

`M = (a+b)/(2)`

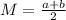
The standard deviation is given by:

`S = \sqrt{((b-a)^2)/(12)}`

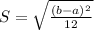
Normal probability distribution

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

The uniform distribution can be approximated to the normal, using its mean and its standard deviation.

Sum of n terms of a normally distributed variable:

The mean of the sum will be:

`\mu_(s) = n\mu`

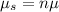
The standard deviation of the sum will be:

`\sigma_(s) = √(n)\sigma`

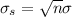
Suppose that the length of research papers is uniformly distributed from 12 to 25 pages.

This means that
`a = 12, b = 25`

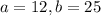
We survey a class in which 55 research papers were turned in to a professor.

This means that
`n = 55`

A.) Give the distribution of X.

The mean has already been given, and the standard deviation is:

`S = \sqrt{((25-12)^2)/(12)} = 3.75`

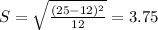
So

X ~ N(18.5, 3.75)

B.) Give the distribution of SumX.

Sum of 55 papers, the standard deviation will be of:

`\sigma_(s) = √(55)*3.75 = 27.8`

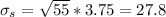
So

SumX ~ N(1017.5,27.8).

C). Calculate the probability that the professor will need to read a total of more than 1080 pages

This is 1 subtracted by the pvalue of Z when X = 1080. So

`Z = (X - \mu_(s))/(\sigma_(s))`

`Z = (1080 - 1017.5)/(27.8)`

`Z = 2.25`

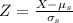
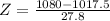
`Z = 2.25` has a pvalue of 0.9878

1 - 0.9878 = 0.0122

0.0122 = 1.22% probability that the professor will need to read a total of more than 1080 pages.