Question

A certain coin is a circle with diameter 18 mm. What is the exact area of either face of the coin in terms of pie?

Answer 1

To find the area of the coin/a circle use this equation:

(a = area, r = radius, d = diameter)

`\text{a = r}^2`

So we need to do for the radius.

`\text{r} = \frac{\text{d}}{2}`

`\text{r} = (18)/(2)`

`\text{r} = 9`

Then solve

`\text{a = 9}^2`

`\boxed{\bold{a = 81}}`

Answer 2

`81\pi`
`mm^2`

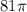
Explanation:

Let's recall the formula for the area of a circle:

`A = \pi r^2`

We are given the diameter, but the formula uses the radius. Since the radius is equal to one-half of the diameter, we can find the radius by doing this:

`r = (1)/(2)d=\\\\r=(1)/(2)(18)= \\\\r=9`

Now that we've found the radius is 9 mm, let's substitute the values into the formula for the area of a circle. We have:

`A = \pi r^2=\\A=\pi (9^2)=\\A=\pi (81)=\\A=81\pi`

So, we've found that the exact area, in terms of pi, of either face of the coin is
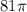
`81\pi`
`mm^2`.