Question

This circle is centered at the point (2, 6), and the length of its radius is 4. What is the equation of the circle?

Answer 1

Option D:
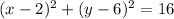`(x-2)^2+(y-6)^2=16` is the equation of the circle.

Step-by-step explanation:

Given that the circle is centered at the point and the length of its radius is 4.

We need to determine the equation of the circle.

The equation of the circle with center and radius r is given by the equation,

`(x-h)^2+(y-k)^2=r^2`

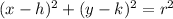
Substituting the center and the radius in the above formula, we get,

`(x-2)^2+(y-6)^2=4^2`

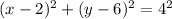
Simplifying the radius, we get,

`(x-2)^2+(y-6)^2=16`

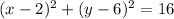
Thus, the equation of the circle is
`(x-2)^2+(y-6)^2=16`

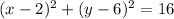
Hence, Option D is the correct answer.