Question

 identify which year the population will reach 0 , help this is due tomorrow

Answer 1

12

Explanation:

As the red wording under the answer box indicates, the population decreases at a constant rate and thus there is a linear relationship between population and time.

In the model P(t) = mt + b, m is the slope and b is the y-intercept.

We can find the slope using the slope formula which is

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`, where x1 and y1 are one point on the line and x2 and y2 are another point on the line.

We know that t is the time since 2010, so one of our points is (0, 6900). Since 2013 is 3 years after 2010, our other point is (3, 5100).

Now, we can simply plug these points into formula, letting the first two represent x1 and y1 and letting the last two represent x2 and y2:

`m=(5100-6900)/(3-0)\\ m=-(1800)/(3)\\ m=-600`

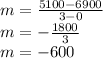
We're already given our y-intercept in the problem (6900) since the y-intercept is when t = 0 and the year and population for t = 0 is 2010 and 6900.

Thus, our model for find the answer is P(t) = -600t + 6900

Because we want to know when the population will reach 0, we can set the equation equal to 0 and solve for t:

`0=-600t+6900\\-6900=-600t\\11.5=t\\12=t`

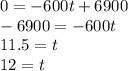
The population will reach 0 in the 12th year or in 2022 (2010 + 12 = 2022)