Question

At the circus, a clown is shot from a cannon. This situation can be modeled by the function: h = – 16t2 + 45t + 15, where 'h' is height in feet and 't' is time in seconds. What is the maximum height of the clown?

A. 45 Feet
B. 109. 4 Feet
C. 72.3 Feet
D. 87.3 Feet

Answer 1

The maximum height is 46.64 feet.

Explanation:

If we take the derivative of h whit respect to t and equal this to zero we would find the value of t which corresponds to the maximum h.

So, we have the function h(t):

`h(t)=-16t^(2) + 45t + 15`

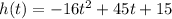
Taking the derivative, we have:

`(dh(t))/(dt)=-32t + 45=0`

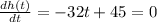
Now, we solve it for t:

`t=(45)/(32)=1.4\: s`

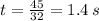
Finally, we put this value of t into the original equation.

`h(t)=-16(1.4)^(2) + 45(1.4) + 15`

`h_(max)=46.64\: ft`

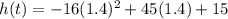
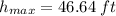
Therefore, the maximum height is 46.64 feet. All the given options are wrong, the one that comes closest is option A.

I hope it helps you!