Question

What are the solutions of this quadratic equation

Answer 1

2x² - 2x - 9 = 0

ax² + bx + c = 0 is the standard form of quadratic equation.

where,

• a = 2
• b = -2
• c = 9

Formula :

`x = \frac{ - b + \sqrt{ {b}^(2) - 4ac } }{2a} \\`

Substituting the values,,

`\sf x = \frac{ - ( - 2) \pm \sqrt{ {( - 2)}^(2) + 4 * ( - 2) * ( - 9) }}{2 * 2 } \\ \\ \sf x = (2 \pm √(4 + 4 * 18 ) )/(4) \\ \\ \sf x = (2 \pm √(4 + 72))/(4) \\ \\ \sf x = (2 \pm √( 76) )/(4) \\ \\`

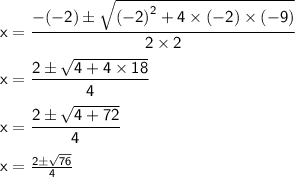
Now, We can simplify √76.

Prime factorisation of √76 is
`√(2 \pm 2 * 19)`

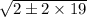
√19 can be written as 4.359.

Now,

`\sf x = ( 2 \pm 2 * 4.359)/(4) \\ \\ \sf x = (2 \pm √(76) )/(4) \\ \\ \sf { \boxed{ \red {x = (1 \pm √(19) )/(2) }}}\\`

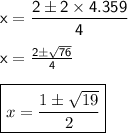
Therefore, Option (C) is the required answer.