Question

How do I do this? None of the tutors know, and I’m really confused… random answers will be reported

Answer 1

a) Turning point(s): (-1, 8), (1, 0), (2.5, 2.5)

x-intercept(s): (-2, 0), (1, 0), (3, 0)

b) negative

c) 4

d) f(x) = -0.5 (x + 2)(x - 1)²(x-3)

Explanation:

a) Determine the number of turning points and any x-intercepts.

Turning points are points at which the function's derivative changes sign. If you haven't gotten to derivatives yet, think about an upward-facing parabola. It has a general U shape and the vertex is the bottom of the parabola. Because the function decreases up until the vertex, then begins to increase from there, the vertex of a parabola is its turning point.

This is a quartic function because it has 4 turns total, so it will have 3 turning points. The turning point is also called a critical point because at this point the derivative of the function is equal to zero. We don't have a function to calculate the crit points from, so we will use the graph. Critical points seem to be at x = -1, 1, 2.5. It is at these places where the function "turns."

The problem also asks for x-intercepts. X-intercepts are places where y = 0. We can look at the graph and see that the x-intercepts are at (-2, 0), (1, 0), and (3, 0).

b) State whether the leader coefficient is positive or negative.

The function opens downward, so the leading coefficient will be negative. Think of an upward opening parabola. Is has a U shape and its formula is
y = x²...A downward facing function (like this one) has an ∩ shape and its formula might be y = -x²...

c) Determine the minimum degree of f.

As stated above, this is a quartic function because there are 4 turns and 3 turning points. Quartic means 4 so the minimum degree of f is 4. The formula should be something like

`f(x) = -x^4...`

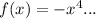
d) Write a function for the graph

The x-intercepts of a function define its formula.

If a line has the equation y = x-4, then the x-intercept is as x = 4. We find this by setting y equal to zero and solving for x. Likewise, you will need to turn the x-intercepts of this function into polynomial factors for our equation.

As we said in Part A, x-intercepts are at x = -2, 1, and 3. So we form the factors of our equation using these numbers. The function "bounces" at
x = 1 because it touches but does not cross the x-axis. This means the (x-1) term needs to be squared.

f(x) = -a ( x + 2 ) ( x - 1 )² ( x - 3 )

f(x) = ( -a ) (x + 2)(x² - 2x + 1)(x - 3)

f(x) = ( -a ) (x² - x - 6) ( x² - 2x + 1)

`f(x) = (-a)(x^4-2x^3+x^2-x^3+2x^2-x-6x^2+12x-6)\\f(x) = (-a)(x^4 -3x^3 -3x^2 +11x - 6)`

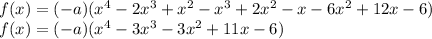
Notice that substituting any of the above values of x makes the equation equal to 0, which means they are x-intercepts of the equation we made.

The variable a represents a scalar for the graph. We know that intercepts are at these points but, many graphs of different heights could have those same intercepts. So we have a graph, meaning we have coordinates to plug into the equation and solve for a. Just remember we can't choose one of the x-intercepts because it will result in a 0. I'm going to use x = 0 to make things simpler.

`f(0) = (-a)(0^4 -3(0^3) -3(0^(2) )+11(0) -6\\f(0) = -6a`

This says that at x = 0, the function is equal to -6a. We look on the graph and see that the function is equal to 3 at x = 0. So...

3 = -6a

a = -0.5

Note that the negative comes from us seeing the graph opening downward.

So the function of the graph is:

f(x) = -0.5 (x + 2)(x - 1)²(x-3)