Question

Find dy/dx for y=4sin²(3x)

Answer 1

24 sin(3x) cos(3x)

Explanation:

To find:-

• The derivative of y = 4sin²(3x) .

Answer:-

The given function to us is ,

`:\sf\implies y = 4sin^2(3x) \\`

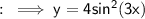
To find it's derivative we would have to use Chain rule of differentiation , which is ;

`:\sf\implies \pink{ (dy)/(dx)=(dy)/(du)\cdot (du)/(dx)} \\`

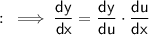
Taking the given function,

`:\sf\implies y = 4sin^2(3x) \\`

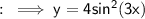
Differentiate both sides with respect to x,

`:\sf\implies (dy)/(dx)=(d)/(dx)4sin^2(3x)\\`

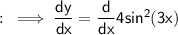
We can take out the constant as ,

`:\sf\implies (dy)/(dx)= 4 (d)/(dx)sin^2(3x) \\`

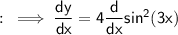
Multiply and divide by sin(3x) as ,

`:\sf\implies (dy)/(dx)= 4 \bigg( (d(sin^23x))/(d(sin3x))* (d\ sin3x)/(dx)\bigg)\\`

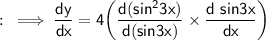
Differentiation of sin(nx) is n cos(nx) and

`:\sf\implies \pink{ (d(x^n))/(dx) = nx^(n-1) }`

So that ,

`:\sf\implies (dy)/(dx)= 4 ( 2sin(3x) \cdot 3cos(3x))\\`

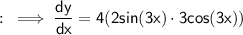
Simplify,

`:\sf\implies\pink{ (dy)/(dx)= 24\ sin(3x) \ cos (3x)}\\`

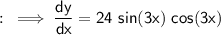
Hence the derivative of the given function is 24 sin(3x) cos(3x) .

`\rule{200}2`

Related formulae :-

`\boxed{\boxed{\begin{minipage}{5cm}\displaystyle\circ\sf\;(d)/(dx)(sin\;x)=cosx \\\\ \circ \;(d)/(dx)(cos\;x) = -sinx \\\\ \circ \; (d)/(dx)(tan\;x) = sec^(2)x \\\\ \circ\; (d)/(dx)(cot\;x) = -csc^(2)x \\\\ \circ \; (d)/(dx)(sec\;x) = secx \cdot tanx \\\\ \circ \; (d)/(dx)(csc\;x) = -cscx \cdot cotx \\\\ \circ\; (d)/(dx)(sinh\;x)=coshx \\\\ \circ\; (d)/(dx)(cosh\;x)= sinhx \\\\ \circ\;(d)/(dx)(tanh\;x)=sech^(2)h \\\\ \circ\;(d)/(dx)(coth\;x)=-csch^(2)x \\\\ \circ\;(d)/(dx)(sech\;x) =-sechx \cdot tanhx \\\\ \circ\;(d)/(dx)(csch\;x) = -cschx \cdot cothx\end{minipage}}}`

`\rule{200}2`

Answer 2

`\frac{\text{d}y}{\text{d}x}=12 \sin (6x)`

Explanation:

To find the derivative of y = 4sin²(3x), use the chain rule.

`\boxed{\begin{minipage}{5.4 cm}\underline{Chain Rule for Differentiation}\\\\If $y=f(u)$ and $u=g(x)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

The given function can be written as:

`y=4(\sin 3x)^2`

Let y = 4u², where u = sin(3x).

Differentiate the two parts separately.

`\frac{\text{d}y}{\text{d}u}=8u \quad \text{and} \quad \frac{\text{d}u}{\text{d}x}=3 \cos (3x)`

Put everything into the chain rule formula:

`\begin{aligned} \implies \frac{\text{d}y}{\text{d}x}& =\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}\\\\&=8u * 3 \cos (3x)\\\\&=24u \cos (3x)\\\\&=24 \sin (3x) \cos (3x) \end{aligned}`

Simplify using the sine double angle identity:

`\boxed{\sin (2 \theta)= 2 \sin \theta \cos \theta}`

`\begin{aligned} \implies \frac{\text{d}y}{\text{d}x}&=24 \sin (3x) \cos (3x) \\\\&=12(2 \sin (3x) \cos (3x))\\\\&=12 \sin (2 \cdot 3x)\\\\&=12 \sin (6x)\end{aligned}`

Therefore:

`\frac{\text{d}y}{\text{d}x}=12 \sin (6x)`

`\hrulefill`

Differentiation Rules

`\boxed{\begin{minipage}{5.8 cm}\underline{Differentiating $ax^n$}\\\\If $y=ax^n$, then $\frac{\text{d}y}{\text{d}x}=nax^(n-1)$\\\end{minipage}}`

`\boxed{\begin{minipage}{5.8 cm}\underline{Differentiating $\sin (ax)$}\\\\If $y=\sin(ax)$, then $\frac{\text{d}y}{\text{d}x}=a \cos (ax)$\\\end{minipage}}`