Question

What is the value of x in the circle on the right?

The value of x is what cm.
(Round to the nearest tenth as needed)​

Answer 1

2.1

Explanation:

Find the number in the tenth place 1 and look one place to the right for the rounding digit 4. Round up if this number is greater than or equal to 5 and round down if it is less than 5.

Answer 2

The value of x in the circle on the right is 5 cm.

Here's how we can find it:

1. Identify the right triangles: Notice that the figure consists of two right triangles. The larger triangle, AEC, has a right angle at E, and the smaller triangle, EBC, also has a right angle at E.

2. Find the length of AE: We are given that AC = 10 cm, and since triangle AEC is a 45-45-90 triangle, we know that AE = AC / sqrt(2). Therefore, AE = 10 cm / sqrt(2) ≈ 7.07 cm.

3. Use the Pythagorean theorem in triangle EBC: We are also given that BC = 6 cm, and we want to find x, which is the length of EB. Applying the Pythagorean theorem, we get:

`x^2 + BE^2 = BC^2`

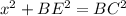
Since BE = AE - AB = 7.07 cm - 5 cm = 2.07 cm, we can plug in the values:

`x^2 + (2.07 cm)^2 = (6 cm)^2`

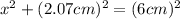
Solving for x, we get:

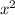`x^2` ≈ 31.64
`cm^2`

x ≈ sqrt(31.64
`cm^2`) ≈ 5.63 cm

4. Round to the nearest tenth: As required, rounding 5.63 cm to the nearest tenth gives us:

x ≈ 5.6 cm ≈ 5 cm