Question

Find the area of the parallelogram below:
What is the area?

Answer 1

The area of the parallelogram is 630.4 square units, to the nearest tenth.

Explanation:

The formula to find the area of a parallelogram is:

`A=bh`

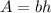
where b is the base and h is the height.

For the given parallelogram ABCD, BC and AD are the bases and h is the height. Therefore, we need to calculate the height, h, before we can calculate the area of the parallelogram.

The height of the parallelogram is also the side opposite angle 62° in the right triangle of the given diagram. As we also know the hypotenuse of this triangle, we can use the sine trigonometric ratio to find "h".

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Given:

• θ = 62°
• O = h
• H = 21

Therefore, the expression for h is:

`\implies \sin 62^(\circ)=(h)/(21)`

`\implies h=21\sin 62^(\circ)`

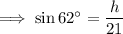
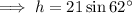
Given the base of the parallelogram is 34 units, substitute b = 34 and the expression for h into the formula for the area:

`\begin{aligned}\implies \textsf{Area}&=34 \cdot 21\sin 62^(\circ)\\&=630.424581...\\&=630.4\; \sf square\;units\;(nearest\;tenth) \end{aligned}`

Therefore, the area of the parallelogram is 630.4 square units, to the nearest tenth.