Question

Refer to trapezoi EFGH WITH MEDIAN IJ if IJ=X,Hg=8 abd EF=12 what is the value of x

Answer 1

x = 10

Explanation:

A trapezoid is a quadrilateral with one pair of parallel sides.

The median of a trapezoid connects the midpoint of the non-parallel sides.

IJ is the median of the trapezoid. I is the midpoint of EH, and J is the midpoint of GF.

Also, the median of a trapezoid is also parallel to the parallel sides. IJ║ HG║ EF.

(The proof of this is extensive and requires drawing additional lines such as HJ and extending EF further until HJ and EF intersect at another point, Y. It is given as the other diagram. You also need prior knowledge of the midsegment of a triangle.)

The measure of the midsegment of a trapezoid, by definition, is also equal to the average of the measure of the parallel segments.

In the figure,

`IJ=((HG+EF))/(2)`

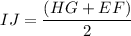
Substituting the values we have, HG = 8, EF = 12 gives us:

`IJ=((HG+EF))/(2)`

`IJ=((8+12))/(2)`

`IJ=(20)/(2)`

`IJ=10`

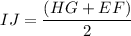
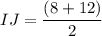
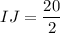
IJ is 10 units.