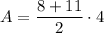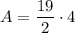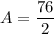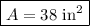Question

Calculate the area of the trapezoid, which is not drawn to scale.

Answer 1

38 in²

Explanation:

We can solve for the area of this trapezoid by using the area formula:

`A = (b_1 + b_2)/(2) \cdot h`

First, we need to identify the trapezoid's bases (
`b_1` and
`b_2`). We know that the bases of a trapezoid are parallel. Using this information, we can identify 8 in and 11 in as the bases.

Next, we need to identify the height (
`h`). We know that the height of a trapezoid is the length from
`b_1` and
`b_2` that is perpendicular (at a right angle) to both of the bases. We can identify this as 4 in because we can see that it adjoins at a right angle to both of them.

Finally, we can plug these values into the area formula and solve for A.

`A = (8 + 11)/(2) \cdot 4`

`A = (19)/(2) \cdot 4`

`A = (76)/(2)`

`\boxed{A = 38 \text{ in}^2}`