Question

From her eye, which stands 1.75 meters above the ground, Myesha measures the angle of elevation to the top of a prominent skyscraper to be 19°. If she is standing at a horizontal distance of 337 meters from the base of the skyscraper, what is the height of the skyscraper? Round your answer to the nearest hundredth of a meter if necessary.

Answer 1

`\large \boxed{ \sf Height= 117.78 \ m }`

Explanation:

We need to find out the height of the skyscraper to thr nearest hundred of metre .

D I A G R A M : -

`\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){4}}\put(0,0.001){\line(0,1){1.5}}\put(0,1.5){\line(2,1){4}}\put(4,0){\line(0,1){3.5}}\put(0,1.501){\line(1,0){4}}\multiput(-1,0.75)(5.1,0){2}{$\sf 1.75 m $}\multiput(2,-0.75)(0,2.5){2}{$\sf 337 m $}\put(4.5,2.2){$\sf x $}\qbezier(0.7,1.5)(0.7,1.7)(0.5,1.75)\put(1,1.67){$\sf 19^\circ $}\put(5,-1.5){$\textcopyright \bf TonyStark $}\put(4, - .5){$\sf C $} \put(4,3.7){$\sf A $} \put(4.1,1.5){$\sf B $} \put( - .5,1.5){$\sf D $} \end{picture}`

Here we can make use of trigonometric ratios to find out the value of firstly AB . In a right angled triangle, tangent is defined as the ratio of perpendicular and base. With respect to angle 19° , the perpendicular is "x" and the base is 337m.

Now in ∆ABD , we have ;

`:\implies\sf tan\theta =(AB)/(BD)\\`

`:\implies\sf tan 19^\circ =( x)/(337\ m) \\`

`:\implies\sf 0.3443=(x)/(337m) \\`

`:\implies\sf x = 337m * 0.3443 \\`

`:\implies\sf \pink{ x =\frak{ 116.03 \ m }} \\`

Now the total height of the skyscraper will be the sum of BC and AB , therefore;

`:\implies\sf height_(skyscraper)= AB + BC \\`

here ,

• BC = 1.75 m .

`:\implies\sf Height_(skyscraper)= (116.03 + 1.75) m\\`

`:\implies\sf \underline{\underline{\boxed{ \sf Height_(skyscraper)= \frak{117.78\ m }}}} \\`

Hence the height of the skyscraper is 117.78 m .

Answer 2

The height of the skyscraper is 117.79 m to the nearest hundredth.

Explanation:

If a person stands at a point and looks up at an object, the angle between their horizontal line of sight and the object is called the angle of elevation.

To find the height of the building, model as a right triangle and solve using the tangent trigonometric ratio. (See the attached diagram).

Tan trigonometric ratio

`\tan \theta=\sf (O)/(A)`

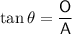
where:

• θ is the angle.
• O is the side opposite the angle.
• A is the side adjacent the angle.

Given information:

• Horizontal distance = 337 m
• Eye level = 1.75 m
• Angle of elevation = 19°

The line of sight is 1.75 m above ground level. Therefore, the height of the skyscraper (the side opposite the angle of elevation) is (y + 1.75) m.

To find y, substitute θ = 19°, O = y and A = 337 into the tan ratio:

`\implies \tan 19^(\circ)=(y)/(337)`

`\implies y=337 \tan 19^(\circ)`

`\implies y=116.038405...`

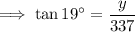
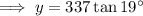
To calculate the height of the skyscraper, add the found value of y to 1.75 m:

`\begin{aligned}\implies \sf Height\;of\;skyscraper&=y+1.75\\&=116.038405... + 1.75\\&= 117.78840...\\&=117.79\; \sf m\;(nearest\;hundredth)\end{aligned}`

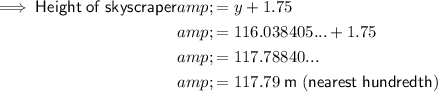
Therefore, the height of the skyscraper is 117.79 m to the nearest hundredth.