Question

The graph of y = h (x) is a dashed green line segment shown below.

Answer 1

Points found on y = h(x) are (7, -6) and (-2,-1).

Using these two points, we will solve for the exact equation of y = h(x).

To solve the equation, we will get the slope (m) of the two points first using the following formula:

`m=(y_2-y_1)/(x_2-x_1) =(-1-(-6))/(-2-7) =(5)/(-9) =-(5)/(9)`

Now that we have a slope, we can now proceed in solving the equation using Point-Slope Formula.

`y-y_1=m(x-x_1)`

`y-(-6)=-(5)/(9)(x-7)`

`y+6=-(5)/(9)(x-7)`

`9y+54=-5x+35`

`9y=-5x+35-54`

`9y=-5x-19`

`y=-(5)/(9)x-(19)/(9)`

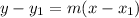
Now that we have the equation of the dashed line, we will now solve for its inverse function y = h^-1 (x).

To solve for the inverse, we will reverse y and x with each other. The new equation will be:

`x=-(5)/(9)y -(19)/(9)`

From that equation, we will now equate or isolate y.

`x=-(5)/(9)y -(19)/(9)`

`x=-(5y-19)/(9)`

`9x=-5y-19`

`5y=-9x-19`

`y=-(9)/(5)x -(19)/(5)`

In this equation, our slope (m) here is -9/5 and our y-intercept is at (0, -19/5). The graph for this equation will look like this.

Drag the endpoints of the solid segment to the coordinates shown above to graph y = h^-1 (x).

Or drag the endpoints to (-6,7) and (-1,-2). It's the same graph anyway.