Question

A rightward force is applied to a 10-kg object to move it across a rough surface at constant velocity.

The coefficient of friction between the object and the surface is 0.2. Use the diagram to determine the
gravitational force, normal force, applied force, frictional force, and net force. (Neglect air resistance.)
Fnorm"
Feriet"
P=0.2
Fgrav".
m - 10 kg
a=0 m/s/s
Fnet
Fapp

Answer 1

***These questions were answered assuming that down and to the left are negative

Constant velocity means that the net force is 0 (you can prove using derivatives).

Fnet = 0 N

The force of gravity can be calculated using the equation Fg = mg.

Fg = mg = 10 (-9.8) = -98 N

Since the force of gravity and the normal force are the only forces in the vertical direction and the net force is 0, they must obey -Fn = Fg (if they don't follow this, the net force will not be 0).

Fn = -Fg = -(-98) = 98 N

The frictional force can calculated using the equation Ff = μFn, where μ is the coefficient of friction.

Ff = μFn = -0.2 (98) = -19.6 N

The force applied can also be calculated using the fact that the net force is 0. For the net force to be 0, the forces in the x direction must cancel (add up to 0), meaning they must be equal magnitude in opposite directions. Therefore Fa = -Ff.

Fa = -Ff = -(-19.6) = 19.6 N

Answer 2

The gravitational force on a 10-kg object is
`\( 98 \, \text{N} \),` normal force is
`\( 98 \, \text{N} \),` frictional force is
`\( 19.6 \, \text{N} \) (due to \( 0.2 \) coefficient of friction), applied force equals frictional force, and the net force is \( 0 \, \text{N} \).`

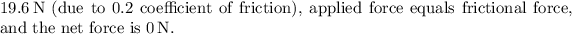
It seems like you mentioned a diagram, but unfortunately, I can't see or interpret visual content. However, I can certainly help you understand the forces at play based on your description.

1. Gravitational Force
`(Weight, \( F_{\text{gravity}} \)):`

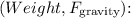
The gravitational force is given by
`\( F_{\text{gravity}} = m \cdot g \),` where
`\( m \)` is the mass of the object (10 kg) and
`\( g \)` is the acceleration due to gravity
`(approximately \( 9.8 \, \text{m/s}^2 \)).`

`\( F_{\text{gravity}} = 10 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 \).`

2. Normal Force
`(\( F_{\text{norm}} \)):`

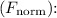
The normal force is the force exerted by a surface that supports the weight of the object resting on it. In this case, since the object is on a horizontal surface and moving at constant velocity, the normal force is equal in magnitude but opposite in direction to the gravitational force.

`\( F_{\text{norm}} = F_{\text{gravity}} \).`

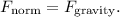
3. Applied Force (\( F_{\text{app}} \)):

The applied force is the force you're applying to move the object. Since the object is moving at constant velocity, the applied force is equal in magnitude but opposite in direction to the frictional force.

`\( F_{\text{app}} = F_{\text{friction}} \).`

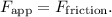
4. Frictional Force
`(\( F_{\text{friction}} \)):`

The frictional force is given by
`\( F_{\text{friction}} = \mu \cdot F_{\text{norm}} \), where \( \mu \)`is the coefficient of friction (0.2).

`\( F_{\text{friction}} = 0.2 \cdot F_{\text{norm}} \).`

5. Net Force (\( F_{\text{net}} \)):

Since the object is moving at constant velocity, the net force is zero. The applied force is balanced by the frictional force.

`\( F_{\text{net}} = 0 \).`

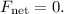
In summary:

`- \( F_{\text{gravity}} = 10 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 \)`

-
`\( F_{\text{norm}} = F_{\text{gravity}} \)`

-
`\( F_{\text{friction}} = 0.2 \cdot F_{\text{norm}} \)`

-
`\( F_{\text{app}} = F_{\text{friction}} \)`

-
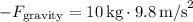
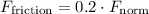
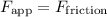
`\( F_{\text{net}} = 0 \)` (since the object is moving at constant velocity)

You can substitute the values to get the numerical results.