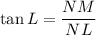Question

In the diagram of right triangle JKL below, KJ║MN. Which of the following ratios is equivalent to tan L?

Answer 1

NM/NL

Explanation:

In the given figure, we can see two triangles, ∆KJL and ∆MNL, which are can be proved similar as,

• ∠LKJ = ∠LMN ( corresponding angles)
• ∠LNM = ∠LJK = 90° ( corresponding angles)
• ∠MLN = ∠KLJ ( common)

Therefore by AAA similarity criterion we can say that both the triangles are similar.

Also we know that the ratio of corresponding sides of two similar triangles are equal.

Now in ∆ KJL ,

==> tanL = p/b

==> tanL = KJ/JL

Now side corresponding to KJ is NM and that to JL is NL . Therefore,

==> tanL = KJ/JL = NM/NL .

Answer 2

`\tan L = (NM)/(NL)`

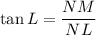
Explanation:

As KJ is parallel to MN, triangle JKL is similar to triangle NML.

In similar triangles, corresponding angles are the same size and corresponding sides are in the same ratio.

The tangent trigonometric ratio is the ratio of the side opposite the angle to the side adjacent the angle in a right triangle:

`\boxed{\tan \theta=\sf (O)/(A)}`

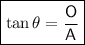
In triangle JKL, side JK is opposite angle L, and side JL is adjacent angle L. Therefore, tan L is:

`\tan L = (JK)/(JL)`

In triangle MNL, NM is opposite angle L, and side NL is adjacent angle L. Therefore, tan L is:

`\tan L = (NM)/(NL)`