Question

Find the exact value of tan U in simplest radical form.

Answer 1

`\large\boxed{\sf tanU =(\sqrt5)/(2)}`

Explanation:

Here we are interested in finding the value of tanU in simplest radical form. From the given right angled triangle, we can see that with respect to angle U , perpendicular is ST and base is UT .

Also the measures of,

• ST = √80
• UT = 8

In a right angled triangle, tangent is defined as the ratio of perpendicular and base . So , we have ;

`\implies \tan\theta = (p)/(b) \\`

`\implies \tan\theta =(ST)/(UT) \\`

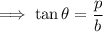
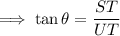
Substitute the respective values ,

`\implies \tan\theta =(√(80))/(8) \\`

Here the angle is U , so that ;

`\implies\tan U =(√(80))/(8) \\`

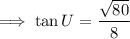
This can we written as ,

`\implies \tan U =(2^2\cdot \sqrt5)/(8) \\`

`\implies \tan U =(4√(5))/(8) \\`

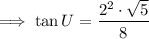
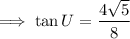
HCF of 4 and 8 is 4 , so on dividing the numerator and denominator by 4 , we have ;

`\implies \underline{\underline{\red{\tan U =(\sqrt5)/(2)}}} \\`

Hence the value of tanU in simplest radical form is √5/2 .

Answer 2

`\tan U=(√(5))/(2)`

Explanation:

To find the exact value of the tangent of an angle in a right triangle, use the tangent trigonometric ratio.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

From inspection of the given right triangle STU, the side opposite angle U is ST, and the side adjacent angle U is UT.

Therefore:

• θ = U
• O = ST = √(80)
• A = UT = 8

Substitute these values into the tangent trigonometric ratio:

`\implies \tan U=(√(80))/(8)`

Rewrite 80 as the product of 16 and 5:

`\implies \tan U=(√(16 \cdot 5))/(8)`

`\textsf{Apply the radical rule:} \quad √(ab)=√(a)√(b)`

`\implies \tan U=(√(16) √(5))/(8)`

Simplify:

`\implies \tan U=(4√(5))/(8)`

Divide the numerator and denominator by 4:

`\implies \tan U=(√(5))/(2)`

Therefore, the exact value of tan U in simplest radical form is:

`\boxed{\tan U=(√(5))/(2)}`