Answer:
Explanation:
The standard form of a line is Ax+By=C. To solve this problem, begin with the point-slope form
 . For this problem, let
. For this problem, let
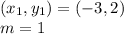
Input these values into the point-slope form equation and convert to slope-intercept form,
![y-(2)=(1)[x-(-3)]\\y-2=x+3\\y-2+2=x+3+2\\y=x+5](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/7zs5eu5pprsy5vkxtaz6.png)
Next, convert slope-intercept form to standard form:
y=x+5
-x+y=5
For standard form, A must be positive. So,
-(x-y)=5
x-y=-5