Question

Please help me with my math!

Answer 1

35 passengers produce the maximum revenue for the bus company.

Explanation:

Define the variables:

• Let "x" be the total number of passengers.
• Let "y" be the total revenue of the bus company (in dollars).

If there are 30 or fewer passengers, each passenger will be charged $80. Therefore, the equation for the total revenue for 30 or fewer passengers is:

`y = 80x,\quad x \leq 30`

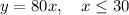
If there are more than 30 passengers, each passenger will be charged $80 minus $2 for every passenger over 30. Therefore, the equation for the total revenue for more than 30 passengers is:

`y = [80 - 2(x - 30)]x, \quad x > 30`

This simplifies to:

`y = [80 - 2x + 60]x, \quad x > 30`

`y = [140 - 2x]x, \quad x > 30`

`y = 140x - 2x^2, \quad x > 30`

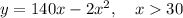
To maximize revenue, we need to find the value of x that maximizes the above equation.

Since this is a quadratic function, the maximum value occurs at the vertex of the parabola.

The x-value of the vertex of a parabola in the form y = ax² + bx + c is when x = - b/2a. Therefore, the x-value of the vertex is:

`\implies x_(\sf vertex)=(-140)/(2(-2))=(-140)/(-4)=35`

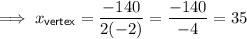
Therefore, the number of passengers that produce the maximum revenue for the bus company is 35.