Question

El area de un rectángulo es 216 m² y su base es 6m mayor que su altura. Determina sus dimensiones recordando la ecuación de segundo grado de la forma ax² + bx + c = 0 y se resuelve con los formula general

Answer 1

`base = 18 m\\\\altura= 12 m`

Explanation:

Disclaimer: My Spanish is not great so I used a translation tool. Please let me know if it is understandable. I think the equations are understandable.

Area = 216 m²

Sea base = b m y altura = h m

`Area = bh`

So

`bh = 216`

base = 6 m mayor que la altura

`b = h + 6`

Así que sustituyendo b en la fórmula bh = 216 da

`b h = 216`

⇒
`(h + 6)h = 216`

⇒
`h^2 + 6h = 216`

⇒
`h^2 + 6h - 216 = 0` [1]

Esta es una ecuación cuadrática que se puede resolver usando fórmulas cuadráticas o factorizando. Aquí se nos pide que utilicemos la fórmula general

Para una ecuación cuadrática general de la forma

`ax^2 + bx + c = 0`

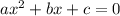
hay dos soluciones dadas por la fórmula cuadrática

`x = ( -b \pm √(b^2 - 4ac))/( 2a )`

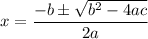
En este problema, comparando
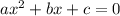`ax^2 + bx + c = 0` a
`h^2 + 6h - 216 = 0` :

`a = 1\\b = 6\\c = -216\\`

Reemplaza estos valores en las fórmulas cuadráticas y resuelve para h

`h = ( -b \pm √(b^2 - 4ac))/( 2a )`

`h = ( -6 \pm √(6^2 - 4(1)(-216)))/( 2(1) )`

`h = ( -6 \pm √(36 - -864))/( 2 )`

`h = ( -6 \pm √(900))/( 2 )`

`h = ( -6 \pm 30\, )/( 2 )`

`h = ( 24 )/( 2 ) \; \; \; h = -( 36 )/( 2 )`

que se convierte

`h = 12`

`h = -18`

Como no podemos tener altura negativa, la solución es

`h = 12` m

Desde b = h + 6,

`b = 12 + 6 = 18 m`