Question

A train decreases speed from 30 m/s to 20 m/s while traveling a distance of 250 m. What is the acceleration of the train?

Answer 1

120/2 = 60km/h »»» (60-48)km/h = 12km/h

Answer 2

The acceleration of the train is
`\(_-2.5 \, \text{m/s}^2\).`

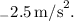
Step-by-step explanation:

The acceleration of the train can be determined using the formula:

`\[a = (\Delta v)/(\Delta t)\]`

where
`\(\Delta v\)` is the change in velocity and
`\(\Delta t\)` is the change in time. In this case, the train decreases its speed from 30 m/s to 20 m/s over a distance of 250 m. To find the change in velocity, subtract the initial velocity from the final velocity:

`\[\Delta v = v_f - v_i = 20 \, \text{m/s} - 30 \, \text{m/s} = -10 \, \text{m/s}\]`

Now, we need to find the time it takes for this change in velocity to occur. We can use the formula:

`\[v = (\Delta x)/(\Delta t)\]`

where v is the average velocity. Rearranging the formula to solve for
`(\Delta t\)`, we get:

`\[\Delta t = (\Delta x)/(v)\]`

Substitute in the given values:

`\[\Delta t = \frac{250 \, \text{m}}{20 \, \text{m/s}} = 12.5 \, \text{s}\]`

Now, plug the values into the acceleration formula:

`\[\Delta t = \frac{250 \, \text{m}}{20 \, \text{m/s}} = 12.5 \, \text{s}\]`

The negative sign indicates that the acceleration is in the opposite direction to the initial velocity, confirming the train is decelerating.