Question

The area of a rectangle is given by the function A(x) = 2x3 + 6x2 + 5x + 15. If the length is defined by x + 3, what is the width of the rectangle?

Answer 1

2x² +5

Explanation:

You want the width of a rectangle with a length of x+3 and an area of A(x) = 2x³ +6x² +5x +15.

Area

The area is the product of length and width, so the width will be ...

A = LW

W = A/L = (2x³ +6x² +5x +15)/(x +3)

The cubic expression can be factored by grouping, so we have ...

Area = (2x³ +6x²) +(5x +15)

= 2x²(x +3) +5(x +3)

= (2x² +5)(x +3)

Then the width is ...

`\text{width}=((x+3)(2x^2+5))/(x+3)=\boxed{2x^2+5}`

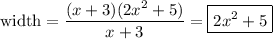
The width of the rectangle is 2x² +5.

<95141404393>