Answer:
108
Explanation:
To find the remainder of the polynomial
 , we can use the Remainder Theorem.
, we can use the Remainder Theorem.
According to the Remainder Theorem, if we divide a polynomial
 by
by
 , the remainder is equal to
, the remainder is equal to
 .
.
In this case,
 .
.
So, substitute
 into the polynomial:
into the polynomial:
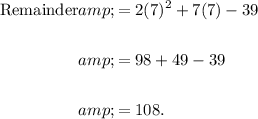
Therefore, the remainder is 108.