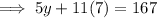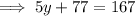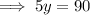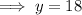Question

NO LINKS!! Please help me with this problem Part 3ee​

Answer 1

Answer: x = 7, y = 18

Explanation:

So we see one angle in the middle is (11x - 9). By vertical angles congruence theorem, the angle vertical to it is also (11x - 9). So the triangle on the right would have the angles (6x - 2), 72, and (11x - 9). The sum of all angles in a triangle is 180, so do 6x - 2 + 72 + 11x - 9 = 180. Solve like this:
6x - 2 + 72 + 11x - 9 = 180 Combine like terms
17x + 61 = 180 Subtract 61 on both sides
17x = 119 Divide by 17 to isolate x
x = 7

Ok so now we know x = 7. We put the sum of all angles on the left triangle to equal to 180. Equation is 30 + 11x - 9 + 5y - 8 = 180.
30 + 11(7) - 9 + 5y - 8 = 180
30 + 77 - 9 + 5y - 8 = 180
90 + 5y = 180
5y = 90
y = 18

Answer 2

x = 7

y = 18

Explanation:

Vertical Angles Theorem

When two straight lines intersect, the vertical angles are congruent.

Interior Angles of a Triangle

The interior angles of a triangle sum to 180°.

Find the value of x by applying both theorems:

`\implies (6x-2)^(\circ)+(11x-9)^(\circ)+72^(\circ)=180^(\circ)`

`\implies 6x-2+11x-9+72=180`

`\implies 17x+61=180`

`\implies 17x=119`

`\implies x=7`

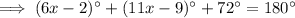
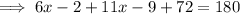
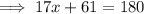
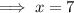
Find the value of y by applying the interior angles theorem:

`\implies (5y-8)^(\circ)+(11x-9)^(\circ)+30^(\circ)=180^(\circ)`

`\implies 5y-8+11x-9+30=180`

`\implies 5y+11x+13=180`

`\implies 5y+11x=167`

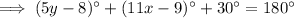
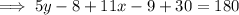
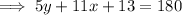
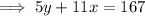
Substitute the found value of x into the equation:

`\implies 5y+11(7)=167`

`\implies 5y+77=167`

`\implies 5y=90`

`\implies y=18`