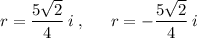Question

0=-16r^2-50
algebra question

Answer 1

`r=(5i√(2) )/(4), -(5i√(2) )/(4)` or simply just say ±
`(5i√(2) )/(4)`.

Hope this helps!

Answer 2

`r=(5√(2))/(4)}\:i\:,\quad \;\;r=-(5√(2))/(4)}\:i`

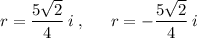
Explanation:

To solve the given equation, rearrange the equation to isolate r.

Given equation:

`0=-16r^2-50`

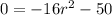
Add 16r² to both sides of the equation:

`0+16r^2=-16r^2-50+16r^2`

`16r^2=-50`

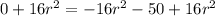
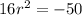
Divide both sides of the equation by 16:

`(16r^2)/(16)=(-50)/(16)`

`r^2=-(25)/(8)`

`\textsf{For\;\:}x^2=f\left(a\right)\textsf{\:the\:solutions\:are\:\:}x=\pm√(f\left(a\right))`

`r=\pm\sqrt{-(25)/(8)}`

`\textsf{Apply\;the\:radical\:rule:}\;\:√(-a)=√(a)√(-1)`

`r=\pm\sqrt{(25)/(8)}√( -1)`

`\textsf{Apply\;the\:imaginary\:number\:rule:}\;\:√(-1)=i`

`r=\pm\sqrt{(25)/(8)}\:i`

`\textsf{Apply\;the\:radical\:rule:}\:\:\sqrt{(a)/(b)}=(√(a))/(√(b)),\:\quad \:a\ge 0,\:b\ge 0`

`r=\pm(√(25))/(√(8))\:i`

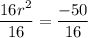
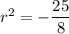
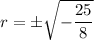
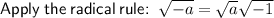
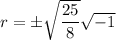
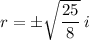
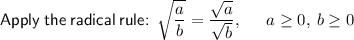
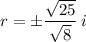
Simplify the numerator and denominator of the fraction:

`r=\pm(5)/(2√(2))\:i`

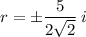
Rationalise the denominator by multiply the numerator and denominator by √2:

`r=\pm(5\cdot√(2))/(2√(2)\cdot √(2))\:i`

`r=\pm(5√(2))/(4)}\:i`

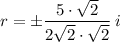
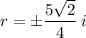
Therefore, the solutions to the given equation are:

`r=(5√(2))/(4)}\:i\:,\quad \;\;r=-(5√(2))/(4)}\:i`