Question

Ruiquelhas asked Mar 23, 2023

254,626 views

1 Answer

Stephopolis · Answer 1 · 2023-03-28T16:39:18+0000

Answer:

See answers in explanation

Explanation:

For 1.)

A.)

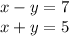
$x-y=7\\x+y=5$

For elimination, attempt to remove one variable. For these problems, the two equations can be added together without modification to remove y:

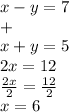
$x-y=7\\+\\x+y=5\\2x=12\\(2x)/(2)=(12)/(2)\\x=6$

Now, substitute x for 6 in equation 2:

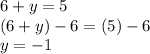
$6+y=5\\(6+y)-6=(5)-6\\y=-1$

To check,

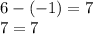
$6-(-1)=7\\7=7$

and

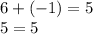
$6+(-1)=5\\5=5$

B.)

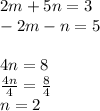
$2m+5n=3\\-2m-n=5\\\\4n=8\\(4n)/(4)=(8)/(4)\\n=2$

Substitute into equation 2:

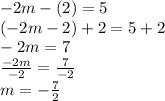
$-2m-(2)=5\\(-2m-2)+2=5+2\\-2m=7\\(-2m)/(-2)=(7)/(-2)\\m=-(7)/(2)$

For part 2, a manipulation must be made for each problem to eliminate a variable:

A.)

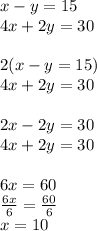
$x-y=15\\4x+2y=30\\\\2(x-y=15)\\4x+2y=30\\\\2x-2y=30\\4x+2y=30\\\\6x=60\\(6x)/(6)=(60)/(6)\\x=10$

Substitute into equation 2:

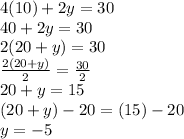
$4(10)+2y=30\\40+2y=30\\2(20+y)=30\\(2(20+y))/(2)=(30)/(2)\\20+y=15\\(20+y)-20=(15)-20\\y=-5$

B.)

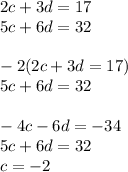
$2c+3d=17\\5c+6d=32\\\\-2(2c+3d=17)\\5c+6d=32\\\\-4c-6d=-34\\5c+6d=32\\c=-2$

Substitute into equation 2:

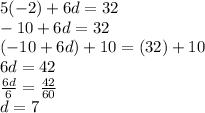
$5(-2)+6d=32\\-10+6d=32\\(-10+6d)+10=(32)+10\\6d=42\\(6d)/(6)=(42)/(60)\\d=7$

For question 3, both equations in each system must be manipulated to eliminate a variable:

A.)

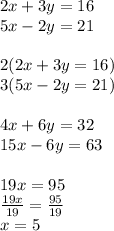
$2x+3y=16\\5x-2y=21\\\\2(2x+3y=16)\\3(5x-2y=21)\\\\4x+6y=32\\15x-6y=63\\\\19x=95\\(19x)/(19)=(95)/(19)\\x=5$

Substitute into equation 2:

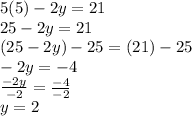
$5(5)-2y=21\\25-2y=21\\(25-2y)-25=(21)-25\\-2y=-4\\(-2y)/(-2)=(-4)/(-2)\\y=2$

B.)

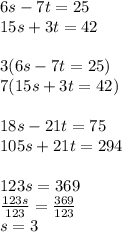
$6s-7t=25\\15s+3t=42\\\\3(6s-7t=25)\\7(15s+3t=42)\\\\18s-21t=75\\105s+21t=294\\\\123s=369\\(123s)/(123)=(369)/(123)\\s=3$

Substitute into equation 2:

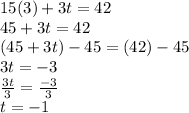
$15(3)+3t=42\\45+3t=42\\(45+3t)-45=(42)-45\\3t=-3\\(3t)/(3)=(-3)/(3)\\t=-1$

I didn't write out all the checks, but all these answers satisfy their original equations. Hope this will help you out.

Your comment on this question: