Question

Two isosceles triangles are joined by making their bases coincide; when this is done

the sum of the lengths of the four sides plus the single "base" is 244 cm. If a
trapezoid is formed from one of the triangles by joining the midpoints of the
congruent sides with a segment that is parallel to the base, the perimeter of the
resulting trapezoid is 106 cm. What are the lengths of the sides and base of the
triangle?

Answer 1

The provided system yields an invalid solution with
`\(a = -138\),` which is infeasible for side lengths. The problem likely contains an error or inconsistency in the given information.

denote the lengths of the congruent sides of each isosceles triangle as
`\(a\)` cm, and the base as
`\(b\)` cm.

Given:

The sum of the lengths of the four congruent sides and the single base is 244 cm:

`\[2a + 2a + b = 244 \implies 4a + b = 244\]`

Forming a trapezoid from one triangle by joining midpoints of the congruent sides with a segment parallel to the base results in a perimeter of 106 cm. In a trapezoid, the mid-segment is half the sum of the bases. Thus, the length of the base of the trapezoid (sum of the congruent sides of the triangle) is
`\(2a\)`. So, the perimeter
`\(106\)` can be expressed as:

`\[2a + 2a + a + b = 106 \implies 5a + b = 106\]`

Now, let's solve this system of equations:

1.
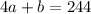
`\(4a + b = 244\)`

2.
`\(5a + b = 106\)`

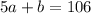
Subtracting equation 1 from equation 2 to eliminate \(b\):

`\[ (5a + b) - (4a + b) = 106 - 244 \]`

`\[ a = -138 \]`

This result for \(a\) seems invalid, indicating an inconsistency in the given information. A negative value for the length of a side of a triangle isn't feasible.

complete the question

"Two isosceles triangles have coinciding bases. The combined sum of their four congruent sides and a single base is 244 cm. Creating a trapezoid from one triangle by joining midpoints of the congruent sides with a segment parallel to the base results in a trapezoid with a perimeter of 106 cm. Find the lengths of the sides and the base of the triangles."