Question

This has 2 parts - The first one is the easy part, the

second parts presents a challenge. You must show
your strategy and calculations to receive full credit.
Write your answer as whole numbers in hours and
in minutes. (Example: 35.25 = 35 hours and 15
minutes (NOTE: every 0.1 hour = 6 minutes))
Part 1: 2 airplanes left the same airport at the same
time. One is traveling at 422 mph straight east, the
other is traveling 384 mph straight west.
How long will it take before they are 6045 miles
apart?
Part 2: 2 airplanes left the same airport at the same
time. One is traveling at 422 mph straight NORTH,
the other is traveling 384 mph straight WEST.
How long will it take before they are 1997 miles
apart?

Answer 1

Explanation:

Part 1)

add their velocities

422+384= 806

now divide 6045 by 806 = 7.5 or 7 hours 30 minutes

7:30 = t hours:minutes

Part 2)

For this part we will need to employ Pythagoras theorem. we need the hypotenuse to be 1,997

so, when will plane traveling N , and plane traveling W be that far (1997)?

or

when does
`1997^(2)` =
`N^(2)` +
`W^(2)`

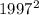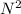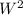
then we're also given that N = 422*t

and that W = 384 * t

so now our formula looks like

`1997^(2)` =
`(422*t)^(2)` +
`(384*t)^(2)`

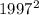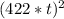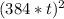
rewrite this so it's making clear math sense

`1997^(2)` =
`422^(2)` *
`t^(2)` +
`384^(2)` *
`t^(2)`

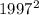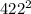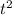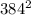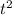
now pull out the
`t^(2)`

`1997^(2)` = (
`422^(2)` +
`384^(2)` ) *
`t^(2)`

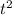
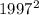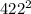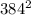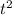
now simplify some

3988009 = (178084 + 147456 ) *
`t^(2)`

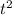
now divide the left side by the numbers on the right

3988009 / (178084 + 147456 ) =
`t^(2)`

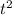
12.12044234 =
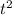
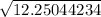`t^(2)`

`√(12.25044234)` = t

3.500063191 = t

so at 3 and a half hours, the planes will be 1997 miles apart

3:30 = t