Question

On Earth, the number flux of solar neutrinos from the p-p chain is:

f_neutrino = 2fo/2.62MeV

Other nuclear reactions in the Sun supplement this neutrino flux with a small additional flux of higher-energy neutrinos. A neutrino detector in Japan, named SuperKamiokande, consists of a tank of 50 kton of water, surrounded by photomultiplier tubes. The tubes detect the flash of Cerenkov radiation emitted by a recoiling electron when a high-energy neutrino scatters on it.

Required:
a. How many electrons are there in the water of the detector?
b. Calculate the detection rate for neutrino scattering, in events per day.

Answer 1

Step-by-step explanation:

The volume of the tank = 50 kton

50 kton = 5 × 10⁷ kg

Since 18 grams of water will contain: 10 electrons × 6.023 × 10²³

Then;

5× 10⁷ kg will contain
`( (5 * 10^7 * 10^3)/(18)) * 10 * 6.023 * 10^(23)`

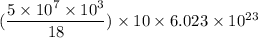
= 1.67 × 10³⁴ electrons

(b)

Suppose:

`f_(neutrino) = (2f_o)/(26.2 MeV) = 6.7* 10^(10) \ s^(-1) cm^(-2)`

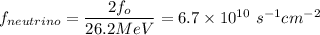
Then;

10⁻⁶ of
`f_(neutrino) = 6.7 * 10^(10) * 10^(-6) \ s^(-1) cm^(-2)`

`=6.7 * 10^(4)\ s^(-1) cm^(-2)`

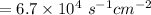
Thus, the number of high energy neutrinos which will interact with water is:

=
`6.7 * 10^4 * \sigma`

=
`6.7 * 10^4 * 10^(-43)`

=
`6.7 * 10^(-39) s^(-1)`

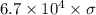
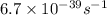
For 1.67 × 10³⁴ electrons, the detection rate is:

`6.7 * 10^(-39) * 1.67 * 10^(34)`

`= 11.19 * 10^(-5) \ s^(-1)`

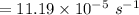
= 9.668 per day