Check the picture below.
so by graphing those two, we get that little section in gray as you see there, now, x = 6 is a vertical line, so we'll have to put the equations in y-terms and this is a washer, so we'll use the washer method.
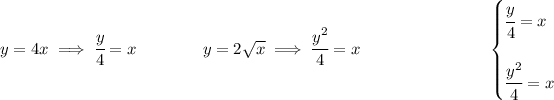
the way I get the radii is by using the "area under the curve" way, namely, I use it to get R² once and again to get r² and using each time the axis of rotation as one of my functions, in this case the axis of rotation will be f(x), and to get R² will use the "farthest from the axis of rotation" radius, and for r² the "closest to the axis of rotation".

now, both lines if do an equation on where they meet or where one equals the other, we'd get the values for y = 0 and y = 1, not surprisingly in the picture.
![\displaystyle\pi \int_0^1\left( 3y-3y^2-\cfrac{y^2}{16}+\cfrac{y^4}{16} \right)dy\implies \pi \left( \left. \cfrac{3y^2}{2} \right]_0^1-\left. y^3\cfrac{}{} \right]_0^1-\left. \cfrac{y^3}{48}\right]_0^1+\left. \cfrac{y^5}{80} \right]_0^1 \right) \\\\[-0.35em] ~\dotfill\\\\ ~\hfill \cfrac{59\pi }{120}~\hfill](https://img.qammunity.org/2023/formulas/mathematics/college/iddc8rcadsclp9wte2qu4ph8h3emzlf9mz.png)