Question

The equation for line g can be written as y–1= – 1/10 (x+8). Parallel to line g is line h, which passes through the point ( – 5,5). What is the equation of line h?

Answer 1

point-slope form:
`y+5=-(1)/(10)(x-5)`

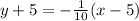
slope-intercept form:
`y = -(1)/(10)x - (9)/(2)`

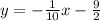
Explanation:

Point-Slope Form:

We can express any one-variable linear equation as:
`y-y_1=m(x-x_1)`, where "m" is the slope, and
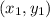`(x_1, y_1)` is some point on the graph.

We're given the equation in point-slope form:
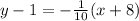`y-1=-(1)/(10)(x+8)`, and if we want to make a line parallel to this line, we just need the slopes to be the same. So let's just look at the value in front of the parenthesis. This is given to be:
`-(1)/(10)`

We can use this same form, to develop an equation parallel to the given line, and passing through:
`(-5, 5)`

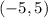
Plugging the values into the point-slope formula, we get:

`y-(-5)=-(1)/(10)(x-5)\\\\y+5=-(1)/(10)(x-5)`

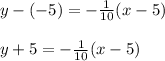
From here we can also convert this into slope-intercept form, where "y" is isolated.

`\\y+5=-(1)/(10)(x-5)\\\\y+5=-(1)/(10)x + (5)/(10)\\\\y + (10)/(2) = -(1)/(10)x + (1)/(2)\\\\y + (10)/(2) - (10)/(2) = -(1)/(10)x + (1)/(2) - (10)/(2)\\\\y = -(1)/(10)x - (9)/(2)`