The object is located approximately 2.53 cm to the left of the converging lens with a focal length of 9.30 cm, forming an erect image 1.90 cm tall on the right side.
To find the object's location, you can use the lens formula:
![\[ (1)/(f) = (1)/(d_o) + (1)/(d_i) \]](https://img.qammunity.org/2024/formulas/physics/high-school/l4mx0hbwqvoq9zbnxbztge1g7edxl72rpg.png)
where:
 is the focal length of the lens,
is the focal length of the lens,
-
 is the object distance (distance from the lens to the object),
is the object distance (distance from the lens to the object),
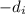 is the image distance (distance from the lens to the image).
is the image distance (distance from the lens to the image).
The sign conventions are as follows:
-
 is positive for converging lenses,
is positive for converging lenses,
-
 is positive for objects on the same side as the incident light (left side for a converging lens),
is positive for objects on the same side as the incident light (left side for a converging lens),
-
 is positive for images formed on the opposite side of the lens from the incident light.
is positive for images formed on the opposite side of the lens from the incident light.
Given:

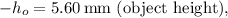

First, convert all measurements to the same unit (centimeters):
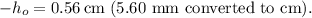
Now, use the magnification formula
 to find
to find
 , where the negative sign indicates an inverted image for the converging lens:
, where the negative sign indicates an inverted image for the converging lens:
![\[ (h_i)/(h_o) = -(d_i)/(d_o) \]](https://img.qammunity.org/2024/formulas/physics/high-school/8h4p7w8x93fn3dgl2flvf67iyopjt5k376.png)
![\[ (1.90)/(0.56) = -(d_i)/(d_o) \]](https://img.qammunity.org/2024/formulas/physics/high-school/v855ea1in9x8o72j9qf54ev0vbbwjs3qoy.png)
![\[ d_i = -(1.90)/(0.56) * d_o \]](https://img.qammunity.org/2024/formulas/physics/high-school/7czzeihxbmn7ffeug0lwf8amdfdunewr09.png)
Now, substitute this expression for
 into the lens formula:
into the lens formula:
![\[ (1)/(f) = (1)/(d_o) - (0.56)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/al6pwqekynps3nshxi1hbeoyquz2k6kdqx.png)
Solve for
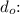
![\[ (1)/(9.30) = (1)/(d_o) - (0.56)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/vvryybjdfco1d4eqytdo102rhfpxd7slun.png)
![\[ (1)/(d_o) = (1)/(9.30) + (0.56)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/5p24wqw8t1vu9h26byh8p54ybyyoihki1w.png)
![\[ (1)/(d_o) = (0.1)/(1) + (0.56)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/uwcf1kgjwq9dxoimao0vtxsi356gmwck9w.png)
![\[ (1)/(d_o) \approx (0.1 * 1.90 + 0.56 * 1)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/l9ih6miidpw4in81dqsj2embefgdp6g5q6.png)
![\[ (1)/(d_o) \approx (0.19 + 0.56)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/hsmbweji3aikmf5ljn5hkdx4ckhngjeidv.png)
![\[ (1)/(d_o) \approx (0.75)/(1.90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/tqa2pmd0gci34nvrdiwvbuddonqzlwusvw.png)
Now, find
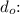
![\[ d_o \approx (1.90)/(0.75) \]](https://img.qammunity.org/2024/formulas/physics/high-school/5s5ad0058f8zfzd0yacrwowo2b0i64781b.png)
![\[ d_o \approx 2.53 \, \text{cm} \]](https://img.qammunity.org/2024/formulas/physics/high-school/l3qzy8puhbu6y98ompjdp3mubnobnlw174.png)
So, the object is located approximately
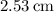 to the left of the converging lens.
to the left of the converging lens.