Answer:
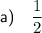

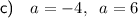
Explanation:
Part (a)
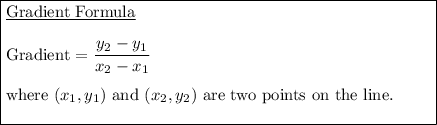
Given points:
- P = (a, a-2)
- Q = (4-3a, -a)
Substitute the given points into the gradient formula to find the gradient of line PQ:
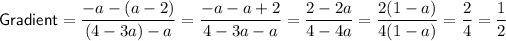
Part (b)
If two lines are perpendicular to each other, their gradients are negative reciprocals.
Therefore, the gradient of a line perpendicular to PQ is:

Part (c)

Substitute the points and the given distance 10√5 into the formula and solve for a.
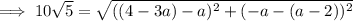
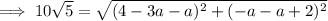
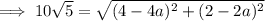
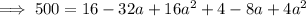
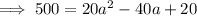
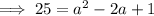
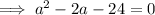
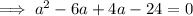
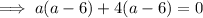
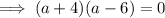
Apply the zero-product property:
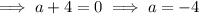
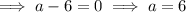
Therefore, the two possible values of a are: