Question

A student concluded that 8x−12=4(12x−6) has infinitely many solutions. Which statement best describes the student’s conclusion? Responses The conclusion is incorrect because the equation has no solution. The conclusion is incorrect because the equation has no solution. The conclusion is incorrect because there is exactly one solution to the equation. The conclusion is incorrect because there is exactly one solution to the equation. The conclusion is correct because there are exactly two solutions to the equation. The conclusion is correct because there are exactly two solutions to the equation. The conclusion is correct because when simplified, both sides of the equation are equivalent. The conclusion is correct because when simplified, both sides of the equation are equivalent.

Answer 1

The conclusion is incorrect because there is exactly one solution to the equation.

Explanation:

8x - 12 = 4(12x - 6)

4 x 12x = 48x 4 x -6 = -24

8x - 12 = 48x - 24

Move the terms

8x - 12 - 48x = -24

Move the constant to the right-hand side and change its sign

8x - 48x = -24 + 12

-40x = -24 + 12

-40x = -12

Divide both sides by -40

40x = -12

40 = 40

x =
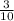`(3)/(10)` or, alternate form, x = 0.3