Question

A business analyst compares 2017 daily sales to 2018 daily sales using descriptive statistics for each. In 2017, the standard deviation of daily sales was 73.87, while in 2018 the standard deviation of daily sales was 136.32. The analyst could conclude that ____________.

Answer 1

The analyst could conclude that there was more variation in sales in 2018.

Step-by-step explanation:

Given

`SD_(2017) = 73.87`

`SD_(2018) = 136.32`

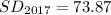
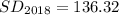
Required

Conclusion about the standard deviations

In statistics, standard deviation gives the average variation in the data being measured.

The standard deviation of 2018 is more than that of 2017. This implies that, in 2018, there is more variation in daily sales compared to 2017

So, the analyst could conclude that there was more variation in sales in 2018.