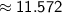Question

Idrk what to put here but can someone help?

Answer 1

Check the picture below.

recall that the acute angles are complementary angles.

`\tan(51^o )=\cfrac{\stackrel{opposite}{AC}}{\underset{adjacent}{7.3}} \implies 7.3\tan(51^o)=AC \implies \boxed{9.0\approx AC} \\\\[-0.35em] ~\dotfill\\\\ \cos(51^o )=\cfrac{\stackrel{adjacent}{7.3}}{\underset{hypotenuse}{AB}} \implies AB\cos(51^o)=7.3 \\\\\\ AB=\cfrac{7.3}{\cos(51^o)}\implies \boxed{AB\approx 11.6}`

Make sure your calculator is in Degree mode.

Answer 2

The measure of Angle Ais
`\sf \boxed{\sf \;\; 39 \;\; }` degrees.

AC is
`\boxed{ \;\;9.0\;\;}` units long.

AB is
`\boxed{\;\; 11.6 \;\;}` units long.

Explanation:

In a right-angled triangle ABC, where C is the right angle, and B is an acute angle, we can use the trigonometric ratios to find the remaining sides and angles.

Given:

• 
  `\sf C = 90^\circ`
• 
  `\sf B = 51^\circ`
• 
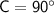
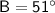
  `\sf BC = 7.3` (the side adjacent to angle B)

Find Angle A:

Since the sum of angles in a triangle is
`\sf 180^\circ`, we can find angle A using the equation:

`\sf A + B + C = 180^\circ`

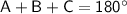
Solve for angle A.

`\sf A = 180^\circ - B - C`

`\sf A = 180^\circ - 51^\circ - 90^\circ`

`\sf A = 39^\circ`

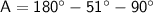
Find Side AC (the side opposite angle B):

Use the tangent ratio (
`\sf \tan`):

`\sf \tan(B) = \frac{\textsf{Opposite}}{\textsf{Adjacent}}`

`\sf \tan(51^\circ) = (AC)/(BC)`

`\sf AC = BC \cdot \tan(51^\circ)`

`\sf AC = 7.3 \cdot \tan(51^\circ)`

`\sf AC \approx 9.014749243`

`\sf AC \approx 9.0 \textsf{(in 1 d.p.)}`

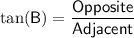
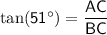
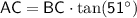
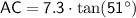
Find Side AB (the hypotenuse):

Use the Pythagorean theorem:

`\sf AB ^2 = AC^2 + BC^2`

`\sf AB = √(AC^2 + BC^2)`

`\sf AB = √((9.014749243)^2+ 7.3^2)`

`\sf AB = √(134.5557039)`

`\sf AB \approx 11.59981482`

`\sf AB \approx 11.6 \textsf{(in 1 d.p.)}`

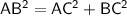
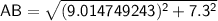
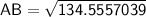
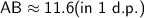
So, the remaining sides and angles are:

• Angle A:
  `\sf 39^\circ`
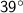
• Side AC:
  `\sf \approx 9.166`
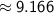
• Side AB:
  `\sf \approx 11.572`