Question

please solve tbis using properties of exponents if you do end up helping me have a blessed day even if you don't still have a bless day​

Answer 1

Using properties of exponents,
`\((x^3y^2/2x^4)^(-2) \:is\: 4x^2y^4\)`

How did we get the value?

Let's simplify the expression using the properties of exponents:

`\((x^3y^2/2x^4)^(-2)\)`

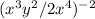
First, apply the reciprocal property of exponents
`(a^(-n) = 1/a^n)`:

`\((1)/((x^3y^2/2x^4)^(2))\)`

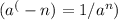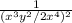
Apply the power of a quotient property of exponents
`\(((a)/(b))^n = (a^n)/(b^n)\)`:

`\((1)/(((x^3y^2)/(2x^4))^2)\)`

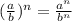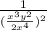
Square the numerator and denominator:

`\((1)/((x^6y^4)/(4x^8))\)`

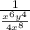
When you divide by a fraction, it's equivalent to multiplying by its reciprocal:

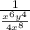`\((1)/((x^6y^4)/(4x^8))\)` is the same as
`\((1)/(1) * (4x^8)/(x^6y^4)\)`

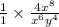
Simplify further:

`\((4x^8)/(x^6y^4)\)`

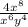
Now, subtract the exponents in the numerator:

`\(4x^(8-6)y^4\)`

`\(4x^2y^4\)`

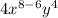
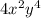
So,
`\((x^3y^2/2x^4)^(-2) = 4x^2y^4\)`