Answer:
UV = 10, ∠ UCT = 44° , ∠ UAV = 20°
Explanation:
• the incentre (V) is equally distant from the triangles three sides
Then
UV = SV = 10
The angle bisector VC , splits ∠ UCT into 2 equal parts
Then
∠ UCT = 2 × ∠ UCV = 2 × 22° = 44°
the sum of the 3 angles in Δ ABC = 180° , that is
∠ SAU + ∠ SBT + ∠ UCT = 180° ( substitute values )
∠ SAU + 96° + 44° = 180°
∠ SAU + 140° = 180° ( subtract 140° from both sides )
∠ SAU = 40°
Since VA bisects ∠ SAU
Then
∠ UAV =
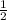 × ∠ SAU =
× ∠ SAU =
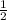 × 40° = 20°
× 40° = 20°