Question

Vertex at (3, 8) and passing through the point (0,-10).

Answer 1

An equation of the quadratic function whose graph has a vertex at (3, 8) and passing through the point (0,-10) is
`f(x) = -2(x - 3)^2 + 8`.

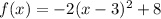In Mathematics and Euclidean Geometry, the vertex form of a quadratic function is represented by the following mathematical equation:

`f(x) = a(x - h)^2 + k`

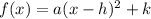
Where:

h and k represents the vertex of the graph.

a represents the leading coefficient.

Based on the information provided above, we can determine the value of a by using the vertex (3, 8) and point or y-intercept (0, -10) as follows:

`f(x) = a(x - h)^2 + k\\\\-10 = a(0 - 3)^2 +8\\\\-10=9a+8\\\\9a=-10-8\\\\a=(-18)/(9)`

a= -2

Therefore, the required quadratic function is given by:

`f(x) = -2(x - 3)^2 + 8`

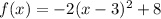
Complete Question:

Write an equation with vertex at (3, 8) and passing through the point (0,-10).