Question

The equation for line s can be written as y+9=–9(x–8). Perpendicular to line s is line t, which passes through the point (9,9). What is the equation of line t?

Write the equation in slope-intercept form. Write the numbers in the equation as simplified proper fractions, improper fractions, or integers.

Answer 1

Line t: y = 1/9x + 8

Explanation:

The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.

The formula for finding the slope the line perpendicular to line s is:

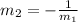`m_(2)=-(1)/(m_(1) )`, where m2 is the slope of the line we don't know (in this case, line t) and m1 is the slope of the line we're given (in this case, line s).

Currently line s is in point-slope form or

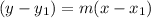`(y-y_(1))=m(x-x_(1))`. Since m is the slope, we know that the slope of line s is -9.

By plugging in -9 for m1 in our equation, we have:

`m_(2)=-(1)/(-9)\\ m_(2)=-(1)/(9)`

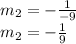
Since we know -1/9 is the slope of line t, we can plug this in for m and (9,9) for x and y in the slope-intercept equation to find b:

`9=1/9(9)+b\\9=1+b\\8=b`

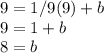
Thus, the equation of line t in slope intercept form is y = 1/9x + 8