Question

11. In the given figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 20cm, to intersect the sides BC, CA and AB at their respective mid-points D, E and F. The area of the shaded region is:​

Answer 1

The area of the shaded region in the equilateral triangle with side length 20 cm, excluding three circular sectors, is
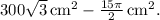`\(300√(3) \, \text{cm}^2 - (15\pi)/(2) \, \text{cm}^2\).` The correct answer is option B.

Step 1 involves identifying the shapes and calculating the area of the equilateral triangle ABC, yielding
`\(100√(3) \, \text{cm}^2\).` Moving to Step 2, the three sectors formed by arcs at vertices A, B, and C are considered. Calculating each sector's area involves determining the radius, central angle, and applying the sector area formula, resulting in
`\((5\pi)/(6) \, \text{cm}^2\)` for each sector.

In Step 3, the shaded region's area is computed by subtracting each sector's area from the corresponding triangle's area at each vertex. The total shaded area, accounting for congruence at each vertex, is expressed as
`\(300√(3) \, \text{cm}^2 - (15\pi)/(2) \, \text{cm}^2\).`

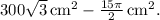
Note that this solution provides an exact answer involving radicals and pi. For a numerical approximation, calculator values for
`\(√(3)\) and \(\pi\)` can be substituted into the final equation.

Therefore, option B is correct.