Step 1: Figure out when Savannah will double her account value:
We need to solve
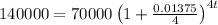 .
.
Divide by 70000:
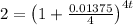
Take the natural log of both sides and bring the exponent down:
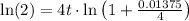
Divide by that mess multiplied by t:
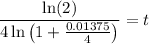
Throw that into a calculator and you get about 50.497297884.
Depending on how picky your teacher is, we'd need to round this to the next time the interest is compounded, since it's only compounded each quarter, so t = 50.5. (The fact is that Savannah's account will never exactly double in value.)
Step 2:
Now, we need to evaluate Carter's continuously compounded investment for 50.5 years:
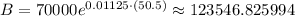
B ≈ 123547 to the nearest dollar.
As a comparison, here's the other calculation with the more precise t value.
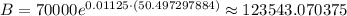
B ≈ 123543 to the nearest dollar.
Again, I would say the 50.5 calculation is actually more correct, since Savannah's account only compounds the interest each quarter, but you'll have to decide what your teacher would say.