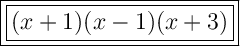Question

What is the complete factorization of the polynomial below?

x³+3x²-x-3
O A. (x-1)(x-1)(x+3)
O B. (x+1)(x-1)(x+3)
OC. (x + 1)(x-1)(x-3)
O D. (x-1)(x-1)(x-3)

Answer 1

B. (x + 1)(x - 1)(x + 3)

Explanation:

To factor the polynomial x³ + 3x² - x - 3, we can start by grouping terms and then using the factoring by grouping method.

Group the first two terms and the last two terms:

`(x^3 + 3x^2) - (x + 3)`

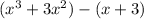
Factor out the greatest common factor from each group:

`x^2(x + 3) - 1(x + 3)`

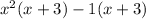
As both groups have a common factor of (x + 3), we can factor out the common factor:

`(x + 3)(x^2 - 1)`

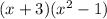
Notice that (x² - 1) is the difference of two squares (x² - 1²).

Therefore, factor (x² - 1) using the difference of two squares formula, a² - b² = (a + b)(a - b):

`(x+3)(x+1)(x-1)`

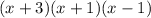
Rearrange the factors to match the order given in the answer options:

`(x+1)(x-1)(x+3)`

So, the factored form of the polynomial x³ + 3x² - x - 3 is:

`\Large\boxed{\boxed{(x+1)(x-1)(x+3)}}`