Question

Determine the equation of the circle with center (0,-7) containing the point (
`√(44)`,-2)

Answer 1

`x^2+(y+7)^2=69`

Explanation:

To determine the equation of the circle with center (0, -7) and containing the point (√(44), -2), we can use the general equation of a circle:

`\boxed{\begin{array}{l}\underline{\textsf{General equation of a circle}}\\\\(x-h)^2+(y-k)^2=r^2\\\\\textsf{where:}\\ \phantom{ww}\bullet\;\textsf{$(h, k)$ is the center.}\\\phantom{ww}\bullet\;\textsf{$r$ is the radius.}\end{array}}`

In this case h = 0 and k = -7, so:

`\begin{aligned}(x-0)^2+(y-(-7))^2&=r^2\\\\x^2+(y+7)^2&=r^2\end{aligned}`

To find the value of r², we can substitute the point (√(44), -2) into the equation:

`\begin{aligned}(√(44))^2+(-2+7)^2&=r^2\\\\44+(5)^2&=r^2\\\\44+25&=r^2\\\\69&=r^2\end{aligned}`

Therefore, the equation of the circle is:

`\large\boxed{\boxed{x^2+(y+7)^2=69}}`

Answer 2

`\sf x^2 + (y + 7)^2 = 69`

Explanation:

The equation of a circle with center
`\sf (h, k)` and radius
`\sf r` is given by the formula:

`\sf (x - h)^2 + (y - k)^2 = r^2`

In this case, the center of the circle is
`\sf (0, -7)`, and it contains the point
`\sf (√(44), -2)`. We can use the distance formula to find the radius (
`\sf r`):

`\sf r = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Substitute the coordinates of the center
`\sf (h, k) = (0, -7)` and the given point
`\sf (x_2, y_2) = (√(44), -2)`:

`\sf r = \sqrt{(√(44) - 0)^2 + (-2 - (-7))^2}`

`\sf r = √(44 + 25)`

`\sf r = √(69)`

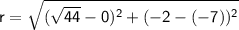
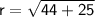
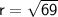
Now, substitute the values of
`\sf h`,
`\sf k`, and
`\sf r` into the circle equation:

`\sf (x - 0)^2 + (y - (-7))^2 = (√(69))^2`

Simplify:

`\sf x^2 + (y + 7)^2 = 69`

So, the equation of the circle with center
`\sf (0, -7)` containing the point
`\sf (√(44), -2)` is:

`\sf x^2 + (y + 7)^2 = 69`