Question

Use the table of points to answer the following questions. x y −6 5 −4 4 1 3 over 2 Part A: What is the slope from (−6, 5) to (−4, 4)? Show every step of your work. (1 point) Part B: What is the slope from (−4, 4) to 1, three halves? Show every step of your work. (1 point) Part C: What do the slopes from Parts A and B tell you about the relationship between all the points in the table? (2 points)

Answer 1

A. The slope from (−6, 5) to (−4, 4) is equal to -1/2.

B. The slope from (−4, 4) to (1, 3/2) is equal to -1/2.

C. The slopes from Parts A and B tell us that the relationship between all the points in the table are linear and represents parallel linear.

In Mathematics and Geometry, the slope of any straight line can be determined by using the following mathematical equation;

Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)

Slope (m) = rise/run

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

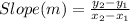
Part A,

By substituting the given data points (−6, 5) to (−4, 4) into the formula for the slope of a line, we have;

Slope (m) = (4 - 5)/(-4 + 6)

Slope (m) = -1/2

Part B,

By substituting the given data points (−4, 4) and (1, 3/2) into the formula for the slope of a line, we have;

Slope (m) = (3/2 - 4)/(1 + 4)

Slope (m) = (-5/2)/5

Slope (m) = -1/2

Part C.

Since the two lines have the same slope, we can logically deduce that they are parallel lines and must be a linear equation with a constant rate of change (slope) of -1/2.