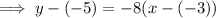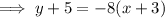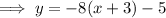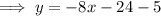Question

Plot four lines to connect the points in adjacent

quadrants. One is done for you.
Line
# 1 y= -2 (x-6)+1
10
# 2?
#3?
#4?

Answer 1

`\textsf{Line \#2}: \quad y=x-5`

`\textsf{Line \#3}: \quad y=(1)/(4)(x-1)-4`

`\textsf{Line \#4}: \quad y=-8x-29`

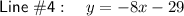
Explanation:

Given points:

• (-4, 3)
• (6, 1)
• (1, -4)
• (-3, -5)

To find the equations for each of the lines:

• Find the slope of the line by substituting two points on the line into the slope formula.
• Substitute the found slope and one of the points on the line into the point-slope formula and simplify.

Line #2

Points:

• Let (x₁, y₁) = (6, 1)
• Let (x₂, y₂) = (1, -4)

Find the slope:

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(-4-1)/(1-6)=(-5)/(-5)=1`

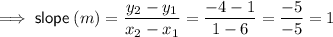
Substitute the found slope and one of the points into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-1=1(x-6)`

`\implies y=(x-6)+1`

`\implies y=x-5`

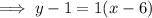
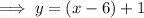
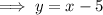
Line #3

Points:

• Let (x₁, y₁) = (1, -4)
• Let (x₂, y₂) = (-3, -5)

Find the slope:

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(-5-(-4))/(-3-1)=(-1)/(-4)=(1)/(4)`

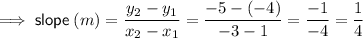
Substitute the found slope and one of the points into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-(-4)=(1)/(4)(x-1)`

`\implies y+4=(1)/(4)(x-1)`

`\implies y=(1)/(4)(x-1)-4`

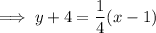
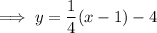
Line #4

Points:

• Let (x₁, y₁) = (-3, -5)
• Let (x₂, y₂) = (-4, 3)

Find the slope:

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(3-(-5))/(-4-(-3))=(8)/(-1)=-8`

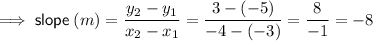
Substitute the found slope and one of the points into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-(-5)=-8(x-(-3))`

`\implies y+5=-8(x+3)`

`\implies y=-8(x+3)-5`

`\implies y=-8x-24-5`

`\implies y=-8x-29`